info@gerb.com
Étude de cas des technologies d’amortissement pour les grands bâtiments : Confort et sécurité
Council on Tall Buildings and Urban Habitat (Conseil sur les grands immeubles et l’habitat urbain, CTBUH), directives relatives aux systèmes d’amortissement
Tour de test Thyssen Krupp, Rottweil/Allemagne
Données relatives au projet
- Année de construction :
2016 (point culminant) - Développeur/Contractant/Propriétaire :
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - Architectes :
Werner Sobek avec JAHN Architects Stuttgart et Chicago - Bureau d’étude structure :
Werner Sobek Stuttgart - Fournisseur des ADAs :
GERB Vibration Control Systems - Bureau d’étude vent :
Wacker Ingenieure (ingénierie du vent / essais en soufflerie) - Hauteur / hauteur entre étage :
246 m / 3,3 m (espaces bureaux) - Elancement :
1/11,8 - Nombre d’étages :
27 niveaux / 8 étages d’espaces bureaux - Superficie brute de la tour :
340 mètres carrés - Fonction du bâtiment :
Tour de test d’ascenseur / bureaux / plateforme d’observation (232 m) - Composition de la structure :
Béton armé (C50/60) / façade avec membrane PTFE sur une structure en acier - Système structurel :
Noyau en béton armé et radier de fondation
(- 32 m) - Technologie d’amortissement employée :
Système d’amortisseur à masse hybride (240 t)

1.0 Introduction/historique
Une tour de 246 m a été érigée au sud-ouest de l’Allemagne avec pour objectif d’accueillir un centre de test et d’innovations dans le domaine des ascenseurs. La tour, qui a une géométrie circulaire avec un diamètre de 20 m, offre suffisamment d’espace pour 9 gaines d’essai, un ascenseur de secour en cas d’incendie et un ascenseur panoramique. En complément, une gaine de 220 m est destiné à être utilisé comme monte charge pour les programmes d’essai.
La base de la tour, de 40 m de diamètre, offre un espace supplémentaire pour des établissements de services, un hall d’entrée et un centre éducatif. A une hauteur de 232 m, une plateforme d’observation (la plus haute d’Allemagne) offre une vue spectaculaire sur la Forêt-Noire et sur les Alpes par temps dégagé.

2.0 Système structurel
Pour l’essentiel, la structure de la tour est constitué d’un tube en béton armé, d’un diamètre de 20,8 m, ancré à une profondeur de 30 m dans le sol environnant (voir figure 2). Jusqu’à une hauteur de 110 m, l’épaisseur du tube est de 40 cm. Au-delà, elle est de 25 cm. Le sol, composé d’une couche de Keuper et de calcaire coquillier, présente une portance élevée, permettant une fondation sur radier. Outre l’ancrage dans le sol environnant, la base plus élargie de la tour offre une rigidité latérale supplémentaire.
La rigidité du tube en béton est principalement apportée par les parois des gaines d’ascenseurs. Des dalles de plancher préfabriquées ont été installées seulement à certains niveaux, afin d’offrir un accès aux gaines d’ascenseurs. Certaines des gaines d’ascenseurs se terminent à un niveau de 115 m et sont recouvertes par une dalle de grande portée coulée en place, d’une épaisseur de 40 cm. Ces étages sont utilisés pour les espaces de bureaux. Au-dessus, un espace vide allant jusqu’à un niveau de 197 m est utilisé comme réservoir de chaleur et pour le système d’ADA. Le haut de la tour est utilisé comme espace de bureau et pour les gaines d’ascenseurs restantes.

L’une des caractéristiques distinctives de la tour de test est sa façade textile, consistant en une maille de fibre de verre recouverte de PTFE. À mesure que l’on monte dans le bâtiment, la largeur d’ouverture de la maille augmente, et avec elle également la transparence de la façade, tandis que la densité et donc le poids du matériau diminuent, améliorant aussi ses propriétés aérodynamiques.
La façade spiralée forme une hélice de Scruton et la toile la composant aide à protéger la structure en béton du soleil, afin de réduire le stress thermique provoqué par les radiations. Pour la conception de la façade et le choix du matériau, les paramètres pris en compte sont l’entretien, la durabilité et la charge de vent.
3.0 Méthode de construction

La tour de test a été érigée selon les étapes suivantes :
- Excavation d’une fosse circulaire de 30 m pour la base de la tour. L’excavation et la forme ont été obtenues grâce à une explosion initiale. Après les travaux d’excavation, la fosse a été sécurisée à l’aide de tirants d’ancrage et d’une paroi en béton projeté.
- Coulage du radier
- Construction du noyau béton verticale à l’aide d’un coffrage coulissant. Les parois ont toutes été construites dans le cadre d’un processus continu sur une période de 4 mois.
- Construction des dalles de plancher.
- Construction de la zone du hall d’entrée.
4.0 Réponse dynamique sous charge de vent
Les fréquences fondamentales de la tour de test calculées étaient de l’ordre de 0,17 Hz à 0,20 Hz par seconde, en fonction de la phase de la construction et de l’état du béton (fissuré/non fissuré), voir figure 4.
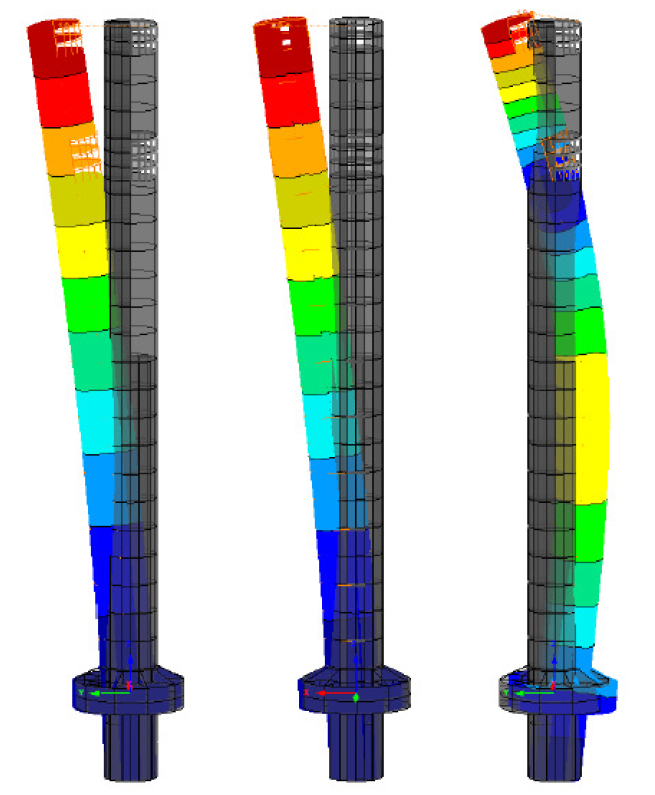
L’étude sous vents a révélée que des vents atteignant une vitesse au sol (à une hauteur de 10 m) de l’ordre de 55 à 60 km/h pouvaient entraîner la mise en résonance de la structure. Il était attendu que, sans amortissement supplémentaire, cette mise en résonnance provoquerait des déflexions d’environ +/- 750 mm au sommet de la structure, entraînant d’une part une gêne pour les occupants, et d’autre part une sollicitation significative en fatigue de la structure en béton de la tour (voir figure 5). Afin de réduire la réponse dynamique à l’excitation provoquée par les vents latéraux, un système d’amortisseur dynamique accordé passif a été mis en place. La tour devant servir de tour de test pour des ascenseurs destinés à des bâtiments sensibles aux oscillations, le propriétaire cherchait la possibilité
d’exciter artificiellement la tour par temps calme, sans que ces mouvements ne provoquent de problèmes liés à la fatigue. Le niveau requis pour les mouvements d’oscillation artificiels était d’approximativement +/- 200 mm, cette plage étant considérée comme sécuritaire. Cette demande nous a offert l’opportunité rare de mettre en place un système d’amortisseur à masse hybride (Hybrid Mass Damper, HMD) ou, le concept étant dévié d’autres systèmes HMD introduits par le passé, un ADA (Tuned Mass Damper, TMD) à double usage. Le système sera présenté dans les chapitres suivants, ainsi que l’optimisation du système passif, la conception du mécanisme de l’actionneur, les algorithmes de contrôle et le concept de sécurité.

5.0 Optimisation du système d'amortisseur dynamique accordé passif
Les paramètres de l’ADA passif doivent être déterminés en fonction de trois aspects distincts : a) ils doivent fournir un amortissement structurel supplémentaire suffisant pour réduire la réponse dynamique liée à l’excitation provoquée par les tourbillons de vent ; b) le déplacement de la masse principale de l’ADA en mode passif doit être limité à une valeur atteignable/pratique lorsqu’elle est soumise à une excitation provoquée par des rafales de vents latéraux ; c) la masse de l’ADA doit être variable pour s’adapter à la déflexion maximale souhaitée de la tour en mode d’excitation, en tenant compte des performances permises par les actionneurs fournis
(p. ex. force induite maximale et course maximale pendant le fonctionnement). Afin d’optimiser l’ADA, un modèle numérique a été utilisé : il représente la distribution de la masse de la tour et les couples d’inertie tels qu’ils sont reportés dans les propriétés structurelles identifiées. Les éléments rigides entre étages ont également été ajustés afin de correspondre aux formes et aux fréquences naturelles relevées à partir d’observations complèmentaires. La fig. 6 de gauche montre les formes et fréquences naturelles de ce modèle analogue employé. La fig. 6 de gauche compare également les formes du modèle analogue à celles du modèle détaillé préparé par le consultant en structures.
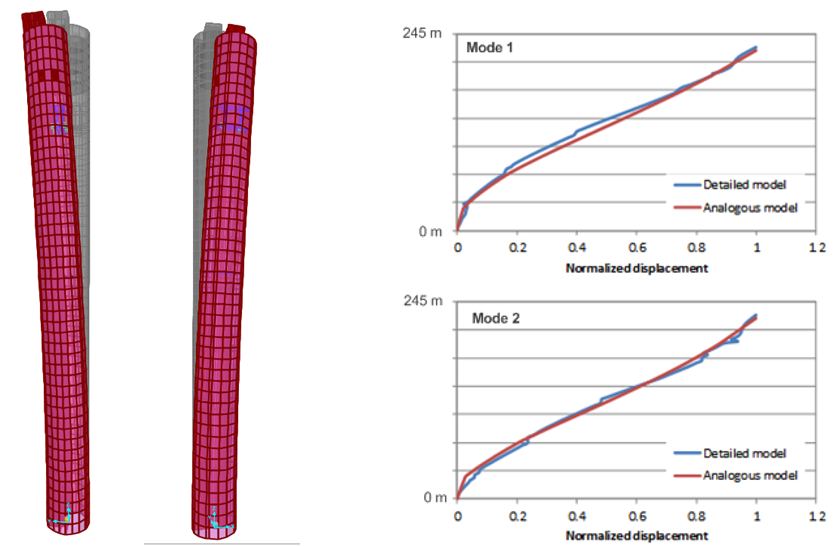
A noter que le TMD a été modelé de façon discrète en tant que système de type pendulaire occupant une place excentrique sur la tour. Les caractéristiques des charges entrantes applicables, c’est à dire l’excitation en résonance provoquée par les tourbillons, sont très similaires à celles d’une excitation harmonique unique. Or, la charge de rafale coexistante est inhérente à sa nature stochastique. C’est pourquoi des critères d’optimisation autres que le très célèbre critère de Den Hartog s’appliquent. De plus, les déplacements relatifs du TMD sont plus importants pour une charge de nature stochastique que pour une charge de type harmonique. Une charge proche de la réalité doit être considérée pour la détermination numérique des paramètres optimaux du TMD. C’est pourquoi un historique temporel a été généré, incluant à la fois les charges de rafales stochastiques (basées sur le spectre de Davenport) et un composant résonnant superposé semblable à un tourbillon, afin de représenter l’excitation globale provoquée par les vents latéraux (voir fig. 3, à droite). La réduction de la déflexion de la tour pouvant être obtenue grâce au système d’ADA optimisé, ainsi que les déplacements de l’ADA correspondants, ils sont illustrés dans la figure 3, à droite.
En se basant sur ces résultats, pour un amortissement structurel inhérent estimé à ξ = 0,8 %, il a été déterminé qu’un ADA d’une masse de 240 t était nécessaire pour maintenir les déplacements dans une plage de +/- 650 mm tout en conservant un ratio d’amortissement optimal offrant les meilleures performances de ce dernier. Un amortissement plus élevé aurait pu permettre de réduire la course tout en gardant une efficacité suffisante, mais cela aurait impacté négativement les exigences en matière de force de l’actionneur. Afin de déterminer les forces nécessaires pour un réglage optimal de l’ADA de 240 t, l’utilisation du modèle analogue a également permis de s’assurer qu’une force maximale de 40 kN des actionneurs permettait d’atteindre une plage de déflexions de la tour de +/- 200 mm. La figure 4 montre les résultats de la simulation numérique dans le domaine temporel sur le modèle numérique analogue ; y sont représentées : les déflexions au niveau du sommet de la tour, les déplacements de la masse de l’ADA et les forces entrantes actives à l’origine de ces déplacements.


6.0 Description du système de contrôle
Le double usage du système de contrôle sert : a) à réduire la consommation d’énergie tout en réduisant les vibrations en fonctionnement passif normal et b) à réduire la puissance d’actionneur nécessaire grâce à l’utilisation des effets de résonnance, afin d’exciter la masse de l’ADA et atteindre en fin de compte le besoin réel en matière de puissance. Les actionneurs servent de liaison entre la structure principale et la masse de TMD, mais à l’inverse d’autres systèmes de contrôle (voir fig. 1), ils ne sont pas utilisés pour contrôler directement la masse du TMD comme le ferait un actionneur de masse actif ou un système d’amortisseurs typiques.
Pour l’ADA à double usage intégré, une masse réactionnelle de 240 t a été choisie pour le fonctionnement passif. Pour le mode excitation, deux entraînements linéaires, un pour chacune des directions principales, sont fixés à la masse du TMD, avec des pivots placés à proximité du centre de gravité de la masse pour éviter les artefacts torsionnels. Chacun des entraînements linéaires peut fournir une force maximale de 40 kN dans une plage de +/- 600 mm maxi (voir détails sur la fig. 2). Les entraînements linéaires peuvent être détachés, de manière à ce que l’intégralité du mode passif ne soit pas influencée par les paliers des actionneurs pour le cas improbable où les paliers seraient défaillants.
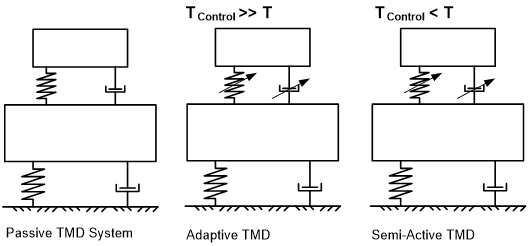
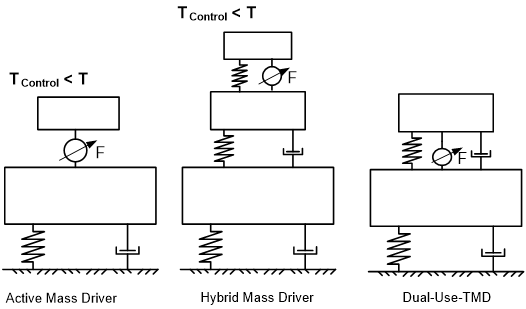
Figure 10 – Types de systèmes de contrôle – TMD à double usage comparé à des systèmes passifs, semi-actifs, actifs et hybrides
Le système est équipé de quatre accéléromètres monoaxes (seismic K-Beam/MEMS ; un dans chaque direction) afin de déterminer les accélérations au niveau du sommet de la tour et de la masse du TMD. Les signaux d’accélération sont dotés de filtres passe-bande à l’intérieur de la plage des fréquences naturelles fondamentales de la tour (comprises entre 0,1 et 0,3 Hz) et intégrés pour obtenir la vitesse et le déplacement de la tour.
De plus, les valeurs de déplacement intégrées peuvent être comparées aux valeurs d’un système de mesure GPS complémentaire installé au sommet de la tour dans le but de comparer les dérives des signaux. Un test de corrélation initial a été réalisé en conséquence. Enfin, les déplacements de l’ADA sont surveillés à l’aide de transducteurs potentiométriques à fil et d’un système inductif de mesure de longueur intégré dans les moteurs linéaires.
7.0 Algorithme de contrôle
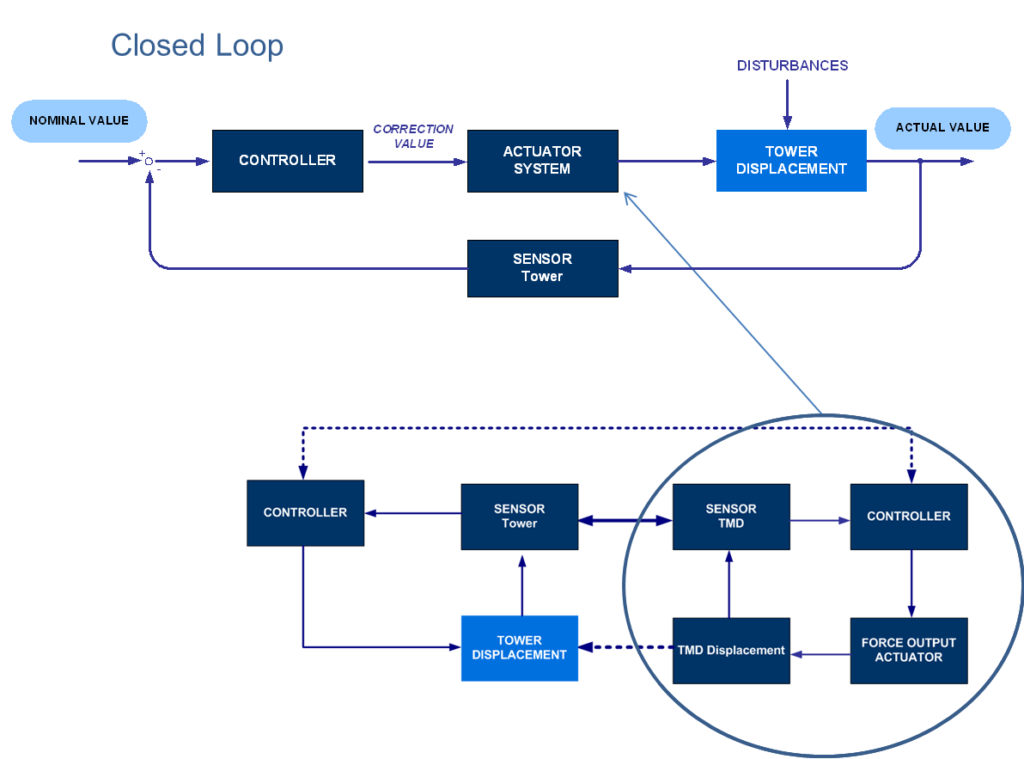
La boucle de contrôle générale de la tour est illustrée à la figure 5 : elle montre la séquence de contrôle de la boucle fermée. Un plan détaillé de l’algorithme de contrôle nécessiterait des modèles analytiques des actionneurs de la masse de l’ADA afin de déterminer la connexion entre l’entrée de l’actionneur et la force d’action appliquée. Un tel modèle devrait être associé au modèle analytique de la structure principale qui décrit le comportement dynamique global du bâtiment. De plus, en comparaison avec les algorithmes de contrôle standard ayant été appliqués à d’autres applications HMD comme dans [2],[3] ou examinés théoriquement comme dans [1] , l’algorithme de contrôle de cette application à cette tour a dû tenir compte de l’excitation contrôlée synchrone dans une direction principale et de la réduction des vibrations dans la direction perpendiculaire. La réponse dynamique étant majoritairement attendue dans les modes fondamentaux, une commande de rétroaction linéaire avec tous ses bénéfices devrait être appliquée pour ces deux tâches afin d’éviter toute instabilité. Pour la commande simple réalisée, la commande de rétroaction linéaire atténuant la réponse dynamique de la tour perpendiculaire à l’excitation règle l’actionneur adéquat à une somme linéaire pondérée spécifique calculée à partir de sept mesures dynamiques structurelles. Les mesures sont : Les accélérations de l’ADA et du sommet de la tour, les vitesses de l’ADA et du sommet de la tour, les déplacements absolues de l’ADA et du sommet de la tour et le déplacement relatif de l’ADA et du sommet de la tour.
Il est important de noter que les facteurs de pondération présélectionnés sont des valeurs scalaires simples, positives ou négatives. Le paramétrage des facteurs de pondération se base sur les tests dynamiques de la tour et n’emploient aucune modification dépendante de la fréquence. La rétroaction de l’actionneur actif est calculée instantanément (à 50 Hz) et il s’agit encore d’une combinaison linéaire des mesures dynamiques précédentes. Aucun manipulation non-linéaire n’est employée. La conception de la commande a également été intégrée dans la simulation numérique d’un domaine temporel (comprendre intégration directe), afin de démontrer la performance de la réduction des vibrations de la commande de l’actionneur. Pour le mode excitation, le même principe a été employé pour la commande, avec une compensation du déplacement qui représente l’excitation de la tour à la valeur de déplacement souhaitée. La compensation est une fonction sinusoïdale basée sur la fréquence fondamentale détectée de chaque direction. La sortie de la commande servant à contrebalancer la variation du déplacement du sommet de la tour provoqué par d’autres perturbations est modulée par la fonction de compensation sinusoïdale et la valeur de la commande est adaptée en conséquence.
La commande de rétroaction linéaire servant à réduire la réponse dynamique de la tour perpendiculaire à l’excitation permet à la commande de la force vers l’actionneur d’être une somme linéaire pondérée spécifique calculée à partir des sept mesures dynamiques du programme. Les sept mesures sont les suivantes : Les accélérations de l’ADA et du sommet de la tour, les vitesses de l’ADA et du sommet de la tour, les déplacements absolues de l’ADA et du sommet de la tour et le déplacement relatif de l’ADA et du sommet de la tour. Il est important de noter que les facteurs de pondération sont des valeurs scalaires simples, positives ou négatives. Le paramétrage du facteur de pondération se base sur les tests dynamiques expérimentaux de la tour. La rétroaction de l’actionneur est activée, calculée instantanément (50 Hz)
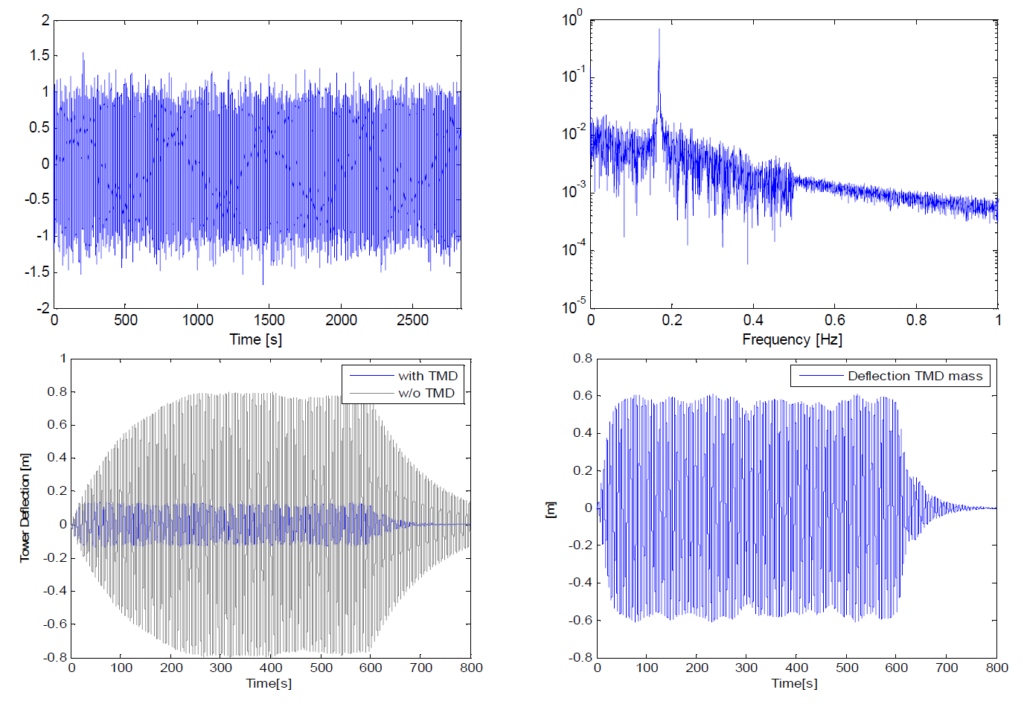
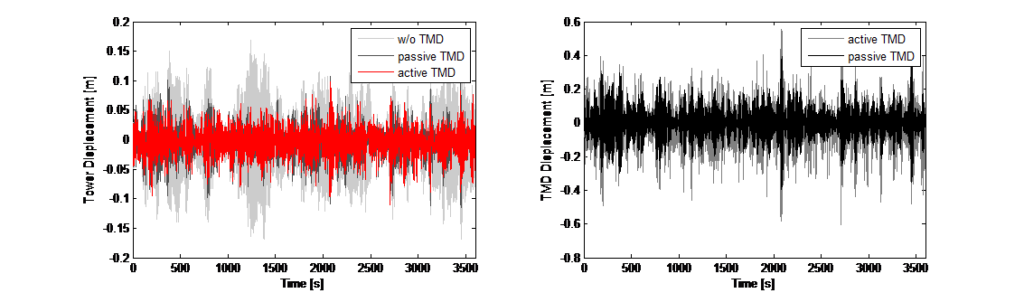
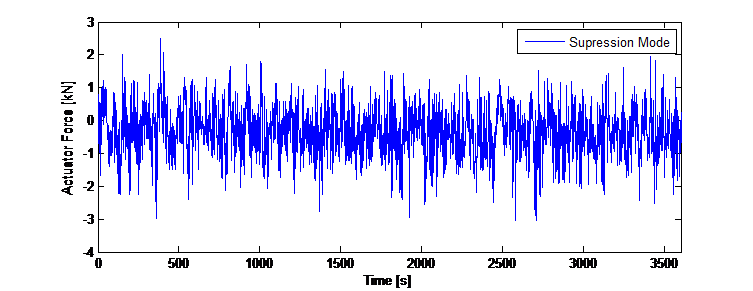
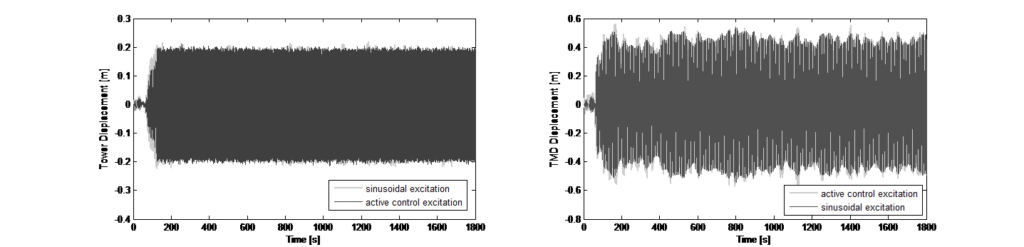
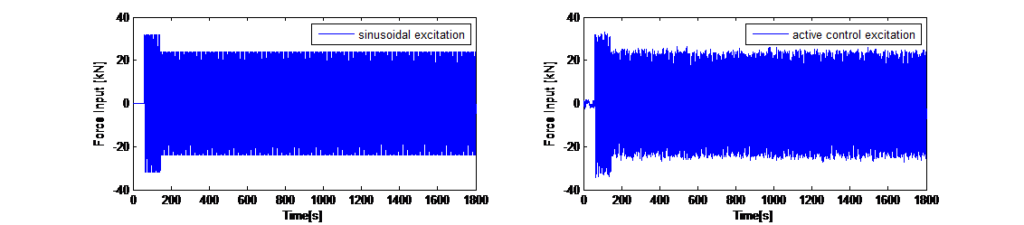
et les facteurs de pondération sont scalaires et n’emploient aucune forme de fonction de transfert liée à la fréquence. La rétroaction est également une combinaison linéaire de la propriété dynamique. Aucun manipulation ou logique non-linéaire n’est employée. La conception de la commande a été intégrée pour une simulation numérique dans le domaine temporel (intégration directe), de sorte que pour chaque stade temporel, l’entrée de force au niveau de la masse du TMD comme commande de l’actionneur peut être adaptée. La figure 12 montre les résultats de la simulation concernant la suppression des vibrations, les déplacements de la tour et la course de la masse du TMD correspondante.
Pour le mode excitation, le même principe a été employé pour la commande, avec une compensation qui représente l’excitation de la tour à la valeur de déplacement souhaitée. La compensation est une fonction sinusoïdale basée sur la fréquence fondamentale détectée de chaque direction. La sortie de la commande servant à contrebalancer la variation du déplacement du haut de la tour provoquée par d’autres perturbations est modulée par la fonction de compensation sinusoïdale
et la valeur de la commande est adaptée en conséquence. Pour cette compensation, un facteur de pondération a été déterminé de manière expérimentale. La figure 13 montre les résultats numériques avec une perturbation liée à une charge de rafale en mode excitation avec une excitation sinusoïdale simple et un algorithme de contrôle appliqué.
8.0 Concept de sécurité
En considérant la force de +/- 40 kN pouvant être fournie par les entraînements linéaires utilisés comme actionneurs, un concept de sécurité est indispensable, afin de s’assurer que les déplacements de la tour n’excèdent pas la résistance en fatigue. Cette condition s’applique, même si la force appliquée n’est pas suffisante pour provoquer des déflexions supérieures aux valeurs prédéfinies de +/- 200 mm au sommet de la tour. L’une des approches visant à améliorer la sécurité du système a consisté à augmenter la redondance des capteurs de surveillance qui enregistrent la déflexion au sommet de la tour. Afin de réaliser au mieux cette tâche, un système de surveillance indépendant additionnel, utilisant idéalement un principe de mesure différent de celui du logiciel de contrôle actuel, a été intégré. Pour le projet présenté ici, le logiciel de contrôle emploie, comme mentionné, des accéléromètres et un niveau d’accélération pour le filtre passe-bande défini à l’intérieur de la plage de fréquences naturelles pertinentes de la structure. Le système de surveillance supérieur principal est un système mondial de navigation par satellites (GNSS) d’une précision de +/- 10 mm.
Le système GNSS requiert une station de base servant de référence qui traite les coordonnées des valeurs de la réponse du déplacement réel. En cas de déplacement du sommet de la tour supérieur à un seuil prédéterminé pendant le mode d’excitation artificiel (ce phénomène pouvant être imputé à une excitation additionnelle par le vent ou autre), un relais commute le signal d’assistance sur 0 V. Ceci entraîne alors l’interruption du mode d’excitation. De plus, les deux systèmes de surveillance contrôlent en continu les données acquises pour s’assurer de l’absence de signaux défectueux des capteurs qui pourraient également entraîner l’interruption du mode d’excitation actif. Les signaux défectueux d’accélération/des transducteurs potentiométriques sont détectés par un critère de sélection d’un pic spectral : on peut supposer que les capteurs fournissent des signaux légitimes uniquement si la sélection du pic dans une plage pertinente est possible. Pendant que le système GNSS analyse le changement de coordonnées, si les données échantillonnées ne changent pas en temps opportun, le système suppose automatiquement que le signal est défectueux.
9.0 Tests de vibrations
Des tests de vibrations initiaux de la tour ont été réalisés avant que la tour ne soit achevée ; à ce stade, les fréquences fondamentales de la tour étaient ainsi supérieures à la plage de réglages spécifiée pour le système TMD passif. Le TMD est ajusté à la fréquence de réglage la plus élevée possible. L’objectif de ces tests de vibrations était de déterminer les fréquences fondamentales de la tour avec un système TMD bloqué, ainsi que l’amortissement structurel inhérent. De plus, le comportement dynamique avec un système TMD passif engagé devrait être déterminé, ainsi que l’augmentation de l’amortissement structurel lié au système d’ADA. Afin d’identifier les fréquences naturelles fondamentales de la tour, il est possible d’employer la méthode de densité spectrale de puissance moyenne normalisée (DSPMN) [1] . Pour cela, les historiques temporels enregistrés doivent être divisés en segments. Ces segments doivent être transformés en domaines de fréquences. Le spectre qui en résulte doit alors être normalisé, la moyenne doit être calculée et le résultat doit être multiplié par le spectre conjugué complexe.
Cette méthode permet d’éliminer toutes les vibrations aléatoires et d’afficher uniquement les vibrations libres récurrentes de la structure dans le spectre moyen qui représente désormais les fréquences naturelles principales en excitation de la tour. La figure 14 de gauche indique les historiques temporels enregistrés des vibrations ambiantes horizontales dans les directions X et Y avec un TMD bloqué. La figure 14 de droite indique la moyenne du spectre d’auto-puissance correspondant pour une longueur de segment de 120 secondes. Le spectre montre que la tour présente une réponse dynamique à deux fréquences dominantes (0,225 Hz dans la direction X et 0,245 Hz dans la direction Y).
Outre la méthode de la moyenne du spectre de puissance décrite ci-dessus, qui suppose que l’excitation ambiante entraîne une réponse dynamique suffisante en modes de vibrations dans l’intérêt d’augmenter la sécurité stochastique, les fréquences naturelles ont été déterminées à l’aide du logiciel commercial de traitement des signaux ARTEMIS [1] qui comprend une méthode de décomposition améliorée du domaine de fréquence et une méthode d’identification du sous-espace stochastique.
La méthode de décomposition améliorée du domaine de fréquence et la méthode d’identification du sous-espace stochastique sont des techniques largement utilisées pour l’identification des paramètres modaux qui concernent uniquement la sortie.
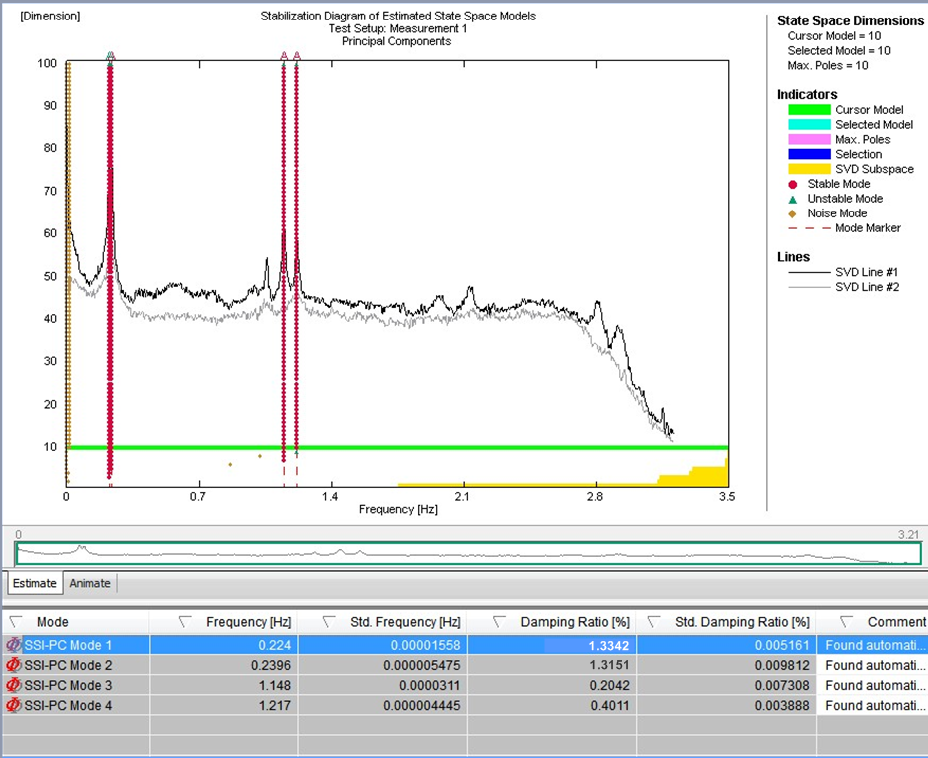
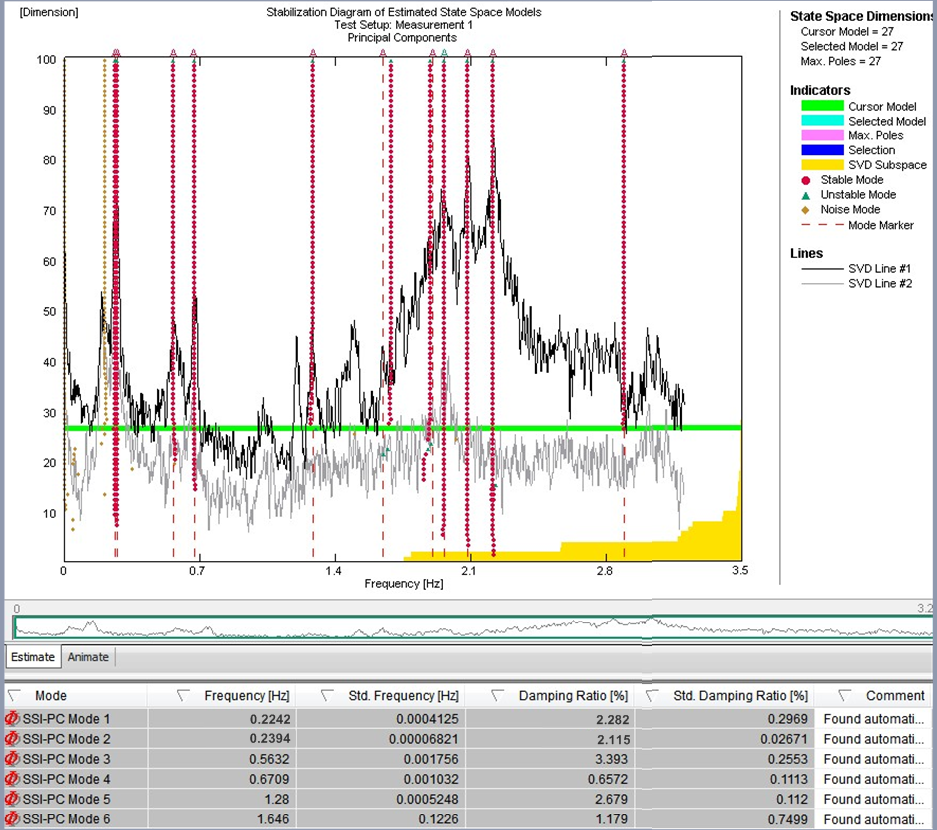
Figure 15 – Fiches de stabilité pour l’enregistrement des vibrations ambiantes avec un TMD bloqué (à gauche) et un TMD activé (à droite)
La méthode de décomposition améliorée du domaine de fréquence repose sur le calcul du spectre de réponses. Des enregistrements longs sont ainsi nécessaires pour maintenir un faible taux d’erreurs concernant l’estimation du spectre et pour permettre une extraction fiable des paramètres modaux. L’algorithme d’identification du sous-espace stochastique a été appliqué afin d’identifier des passerelles à l’aide d’un modèle qui concerne uniquement la sortie. Les méthodes d’identification du sous-espace stochastique fonctionnent sous forme de domaines temporels et se basent sur une description de l’espace-état du problème dynamique. Les résultats de l’identification du système à différents ordres du modèle sont comparés afin de distinguer les modes structurels réels des modes simulés dans les diagrammes de stabilisation. Ces diagrammes sont une méthode appréciée de sélection du modèle de système, car les modes structurels réels tendent à rester stables pour les ordres de modèles successifs et remplissent certains critères de stabilisation évalués dans des procédures automatisées. La figure 15 montre une fiche de stabilité pour des données ambiantes enregistrées à partir desquelles les modes pertinents n’ont pas pu être déterminés. Les modes identifiés et les ratios d’amortissement déterminés pour chaque mode avec TMD bloqué (à gauche) et TMD activé (à droite) sont également illustrés sur la figure 14. Une augmentation de l’amortissement structurel peut être observée. L’amortissement structurel additionnel se trouve dans la plage de valeurs théoriques pouvant être déterminées à partir du modèle théorique pour lequel le réglage de TMD désaccordé a été envisagé.
Outre les tests de vibrations ambiantes avec le système de TMD passif, des tests préliminaires avec le mode d’excitation actif ont été réalisés, alors que le système TMD était désaccordé. La figure 12 de gauche illustre l’historique temporel des accélérations enregistrées au sommet de la tour. Après l’excitation sinusoïdale initiale, l’algorithme permettant d’atteindre un niveau d’accélération constant a été activé, afin de déterminer de manière expérimentale la corrélation entre la déflexion de la tour et le déplacement forcé de la masse du TMD. L’historique temporel illustré à la figure 12 montre les deux scénarios d’essai en mode d’excitation et le spectre TFD correspondant montre la réponse claire de la tour dans ses deux fréquences fondamentales (directions X et Y). La section temporelle marquée en vert correspond à une excitation sinusoïdale de la masse avec commande active désactivée ayant entraîné une réponse dynamique dans les deux directions principales. Le spectre TFD qui en résulte montre les deux pics permettant d’identifier les fréquences fondamentales dans ces deux directions. Le segment temporel marqué en bleu correspond à une excitation avec commande active activée ayant entraîné un déplacement plus constant de la tour, principalement dans une direction. La réduction des vibrations inhérentes une fois le mode d’excitation désactivé a également été utilisée pour déterminer l’amortissement structurel défini à D = 2,4 %. Ce résultat corrèle le ratio d’amortissement déterminé avec les algorithmes d’identification des sous-espaces stochastiques.
10.0 Conclusion et perspectives
Un ADA à double usage a été installé sur la tour de test Thyssen Krupp d’une hauteur de 246 m, avec pour objectif de pouvoir exciter artificiellement la tour et ainsi d’obtenir une réponse dynamique contrôlée dans ses fréquences fondamentales. L’objectif de cette excitation est d’obtenir une oscillation définie du bâtiment dans les deux directions principales de la tour. Sur la base de calculs numériques, il a été déterminé qu’une masse de TMD de 240 t était nécessaire pour atteindre l’amortissement supplémentaire requis pour le mode passif et générer la force de contrôle requise permettant d’obtenir un déplacement du haut de la tour de +/- 200 mm. Afin de créer un niveau de déplacement constant en mode d’excitation et d’éliminer les déplacements provoqués par les vents et les composants à l’origine des vibrations forcées dans la direction perpendiculaire, un algorithme de contrôle a été développé et testé à l’aide de simulations numériques. Après l’installation du système d’ADA passif de type pendulaire pour lequel des dalles de béton préfabriquées ont été utilisées afin de servir de masse réactionnelle, les actionneurs ont été commandés et des tests initiaux ont été réalisés. Les tests ont révélé que l’amortissement inhérent de la tour était plus élevé que ce qui avait été anticipé, mais que tous les modes pertinents pouvaient être clairement déterminés. Le système d’excitation actif du bâtiment a pu être testé et il fonctionne convenablement. Le bâtiment n’étant pas encore entièrement achevé à ce moment, il n’a cependant pas été testé dans toute son ampleur pour permettre d’obtenir l’ensemble des paramètres de fonctionnement. En raison de l’état inachevé du bâtiment, le TMD passif n’a pas pu être adapté aux fréquences fondamentales déterminées.
Une fois que le système d’amortissement sera ajusté, des tests supplémentaires du bâtiment seront réalisés. Ils incluront également des tests concernant l’amortissement en fonction de l’amplitude et l’intégration des systèmes de sécurité.
RÉFÉRENCES
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
Ressources supplémentaires
Vous souhaitez de plus amples informations à ce sujet ?
N'hésitez pas à nous contacter et à nous poser vos questions.
L'un de nos ingénieurs projet vous répondra dans les plus brefs délais.
Étude de cas des technologies d'amortissement pour les grands bâtiments : Confort et sécurité
Council on Tall Buildings and Urban Habitat (Conseil sur les grands immeubles et l’habitat urbain, CTBUH), directives relatives aux systèmes d’amortissement
Tour de test Thyssen Krupp, Rottweil/Allemagne
Données relatives au projet
- Année de construction :
2016 (point culminant) - Développeur/Contractant/Propriétaire :
Krupp Hoesch Stahl GmbH / Thyssen Krupp Elevators - Architectes :
Werner Sobek avec JAHN Architects Stuttgart et Chicago - Bureau d’étude structure :
Werner Sobek Stuttgart - Fournisseur des ADAs :
GERB Vibration Control Systems - Bureau d’étude vent :
Wacker Ingenieure (ingénierie du vent / essais en soufflerie) - Hauteur / hauteur entre étage :
246 m / 3,3 m (espaces bureaux) - Nombre d’étages :
27 niveaux / 8 étages d’espaces bureaux - Superficie brute de la tour :
340 mètres carrés - Fonction du bâtiment :
Tour de test d’ascenseur / bureaux / plateforme d’observation (232 m) - Technologie d’amortissement employée :
Système d’amortisseur à masse hybride (240 t)

- Composition de la structure :
Béton armé (C50/60) / façade avec membrane PTFE sur une structure en acier - Système structurel :
Noyau en béton armé et radier de fondation
(- 32 m)
Étude de cas des technologies d'amortissement pour les grands bâtiments : Confort et sécurité
Council on Tall Buildings and Urban Habitat (Conseil sur les grands immeubles et l’habitat urbain, CTBUH), directives relatives aux systèmes d’amortissement
Tour de test Thyssen Krupp, Rottweil/Allemagne
Données relatives au projet
- Année de construction : 2016 (achevement)
- Développeur/Contractant/Propriétaire : Krupp Hoesch Stahl GmbH/Thyssen Krupp Elevators
- Concepteur architectural : Werner Sobek avec JAHN Architects Stuttgart et Chicago
- Concepteur structurel : Werner Sobek Stuttgart
- Fournisseur de la technique d'amortissement : GERB Vibration Control Systems
- Bureau d’étude vent : Wacker Ingenieure (ingénierie du vent / essais en soufflerie)
- Hauteur/hauteur entre les étages : 246 m/3,3 m (espaces bureaux)
- Étages : 27 niveaux / 8 étages d'espaces bureaux
- Superficie brute de la tour : 340 mètres carrés
- Fonction du bâtiment : Tour de test d'ascenseur/bureaux/plateforme d'observation (232 m)
- Matériau structurel : Béton armé (C50/60) / façade avec membrane PTFE sur une structure en acier
- Système structurel : Noyau de béton armé un radier de fondation (- 32 m)
- Technologie d'amortissement employée : Système d'amortisseur à masse hybride (240 t)

1.0 Introduction/historique
Une tour de 246 m a été érigée au sud-ouest de l’Allemagne avec pour objectif d’accueillir un centre de test et d’innovations dans le domaine des ascenseurs. La tour, qui a une géométrie circulaire avec un diamètre de 20 m, offre suffisamment d’espace pour 9 gaines d’essai, un ascenseur de secour en cas d’incendie et un ascenseur panoramique. En complément, une gaine de 220 m est destiné à être utilisé comme monte charge pour les programmes d’essai.
La base de la tour, de 40 m de diamètre, offre un espace supplémentaire pour des établissements de services, un hall d’entrée et un centre éducatif. A une hauteur de 232 m, une plateforme d’observation (la plus haute d’Allemagne) offre une vue spectaculaire sur la Forêt-Noire et sur les Alpes par temps dégagé.

2.0 Système structurel
Pour l’essentiel, la structure de la tour est constitué d’un tube en béton armé, d’un diamètre de 20,8 m, ancré à une profondeur de 30 m dans le sol environnant (voir figure 2). Jusqu’à une hauteur de 110 m, l’épaisseur du tube est de 40 cm. Au-delà, elle est de 25 cm. Le sol, composé d’une couche de Keuper et de calcaire coquillier, présente une portance élevée, permettant une fondation sur radier. Outre l’ancrage dans le sol environnant, la base plus élargie de la tour offre une rigidité latérale supplémentaire.
La rigidité du tube en béton est principalement apportée par les parois des gaines d’ascenseurs. Des dalles de plancher préfabriquées ont été installées seulement à certains niveaux, afin d’offrir un accès aux gaines d’ascenseurs. Certaines des gaines d’ascenseurs se terminent à un niveau de 115 m et sont recouvertes par une dalle de grande portée coulée en place, d’une épaisseur de 40 cm. Ces étages sont utilisés pour les espaces de bureaux. Au-dessus, un espace vide allant jusqu’à un niveau de 197 m est utilisé comme réservoir de chaleur et pour le système d’ADA. Le haut de la tour est utilisé comme espace de bureau et pour les gaines d’ascenseurs restantes.

L’une des caractéristiques distinctives de la tour de test est sa façade textile, consistant en une maille de fibre de verre recouverte de PTFE. À mesure que l’on monte dans le bâtiment, la largeur d’ouverture de la maille augmente, et avec elle également la transparence de la façade, tandis que la densité et donc le poids du matériau diminuent, améliorant aussi ses propriétés aérodynamiques.
La façade spiralée forme une hélice de Scruton et la toile la composant aide à protéger la structure en béton du soleil, afin de réduire le stress thermique provoqué par les radiations. Pour la conception de la façade et le choix du matériau, les paramètres pris en compte sont l’entretien, la durabilité et la charge de vent.
3.0 Méthode de construction

La tour de test a été érigée selon les étapes suivantes :
- Excavation d’une fosse circulaire de 30 m pour la base de la tour. L’excavation et la forme ont été obtenues grâce à une explosion initiale. Après les travaux d’excavation, la fosse a été sécurisée à l’aide de tirants d’ancrage et d’une paroi en béton projeté.
- Coulage du radier
- Construction du noyau béton verticale à l’aide d’un coffrage coulissant. Les parois ont toutes été construites dans le cadre d’un processus continu sur une période de 4 mois.
- Construction des dalles de plancher.
- Construction de la zone du hall d’entrée.
4.0 Réponse dynamique sous charge de vent
Les fréquences fondamentales de la tour de test prévues étaient de l’ordre de 0,17 Hz à 0,20 Hz par seconde, en fonction de la phase de la construction et de l’état du béton (fissuré/non fissuré), voir figure 4.

L’étude sous vents a révélée que des vents atteignant une vitesse au sol (à une hauteur de 10 m) de l’ordre de 55 à 60 km/h pouvaient entraîner la mise en résonance de la structure. Il était attendu que, sans amortissement supplémentaire, cette mise en résonnance provoquerait des déflexions d’environ +/- 750 mm au sommet de la structure, entraînant d’une part une gêne pour les occupants, et d’autre part une sollicitation significative en fatigue de la structure en béton de la tour (voir figure 5). Afin de réduire la réponse dynamique à l’excitation provoquée par les vents latéraux, un système d’amortisseur dynamique accordé passif a été mis en place. La tour devant servir de tour d’essai pour des ascenseurs destinés à des bâtiments sensibles aux oscillations, le propriétaire cherchait la possibilité d’exciter artificiellement la tour par temps calme, sans que ces mouvements ne provoquent de problèmes liés à la fatigue. Le niveau requis pour les mouvements d’oscillation artificiels était d’approximativement +/- 200 mm, cette plage étant considérée comme sécuritaire. Cette demande nous a offert l’opportunité rare de mettre en place un système d’amortisseur à masse hybride (Hybrid Mass Damper, HMD) ou, le concept étant dévié d’autres systèmes HMD introduits par le passé, un ADA (Tuned Mass Damper, TMD) à double usage. Le système sera présenté dans les chapitres suivants, ainsi que l’optimisation du système passif, la conception du mécanisme de l’actionneur, les algorithmes de contrôle et le concept de sécurité.

5.0 Optimisation du système d'amortisseur dynamique accordé passif
Les paramètres du système TMD passif doivent être déterminés en fonction de trois aspects distincts : a) ils doivent fournir un amortissement structurel supplémentaire suffisant visant à réduire la réponse dynamique liée à l’excitation provoquée par les tourbillons ; b) ils doivent limiter le déplacement de la masse principale du TMD en mode passif à une valeur atteignable/pratique lorsqu’elle est soumise à une excitation provoquée par des rafales de vents latéraux ; c) ils doivent permettre de choisir la masse du TMD en fonction de l’apport énergétique nécessaire à la déflexion maximale souhaitée de la tour en mode d’excitation, en tenant compte de l’enveloppe de performances permise par les actionneurs fournis (p. ex. force générée maximale et course maximale pendant le fonctionnement). Afin d’optimiser l’ADA, un modèle numérique a été utilisé : il représente la distribution de la masse de la tour et les couples d’inertie tels qu’ils sont reportés dans les propriétés structurelles identifiées. Les éléments rigides entre étages ont également été ajustés afin de correspondre aux formes et aux fréquences naturelles relevées à partir d’observations complèmentaires. La fig. 6 de gauche montre les formes et fréquences naturelles de ce modèle analogue employé. La figure 6 de gauche compare également les formes du modèle analogue à celles du modèle détaillé préparé par le consultant en structures.


A noter que le TMD a été modelé de façon discrète en tant que système de type pendulaire occupant une place excentrique sur la tour. Les caractéristiques des charges entrantes applicables, c’est à dire l’excitation en résonance provoquée par les tourbillons, sont très similaires à celles d’une excitation harmonique unique. Or, la charge de rafale coexistante est inhérente à sa nature stochastique. C’est pourquoi des critères d’optimisation autres que le très célèbre critère de Den Hartog s’appliquent. De plus, les déplacements relatifs du TMD sont plus importants pour une charge de nature stochastique que pour une charge de type harmonique. Une charge proche de la réalité doit être considérée pour la détermination numérique des paramètres optimaux du TMD. C’est pourquoi un historique temporel a été généré, incluant à la fois les charges de rafales stochastiques (basées sur le spectre de Davenport) et un composant résonnant superposé semblable à un tourbillon, afin de représenter l’excitation globale provoquée par les vents latéraux (voir fig. 3, à droite). La réduction de la déflexion de la tour pouvant être obtenue grâce au système TMD passif optimisé, ainsi que les déplacements du TMD correspondants, sont illustrés dans la figure 3, à droite.
En se basant sur ces résultats, pour un amortissement structurel inhérent estimé à ξ = 0,8 %, il a été déterminé qu’un ADA d’une masse de 240 t était nécessaire pour maintenir les déplacements dans une plage de +/- 650 mm tout en conservant un ratio d’amortissement optimal offrant les meilleures performances de ce dernier. Un amortissement plus élevé aurait pu permettre de réduire la course tout en gardant une efficacité suffisante, mais cela aurait impacté négativement les exigences en matière de force de l’actionneur. Afin de déterminer les forces nécessaires pour un réglage optimal de l’ADA de 240 t, l’utilisation du modèle analogue a également permis de s’assurer qu’une force maximale de 40 kN des actionneurs permettait d’atteindre une plage de déflexions de la tour de +/- 200 mm. La figure 4 montre les résultats de la simulation numérique dans le domaine temporel sur le modèle numérique analogue ; y sont représentées : les déflexions au niveau du sommet de la tour, les déplacements de la masse de l’ADA et les forces entrantes actives à l’origine de ces déplacements.


6.0 Description du système de contrôle
Le double usage du système de contrôle sert : a) à réduire la consommation d’énergie tout en réduisant les vibrations en fonctionnement passif normal et b) à réduire la puissance d’actionneur nécessaire grâce à l’utilisation des effets de résonnance, afin d’exciter la masse de l’ADA et atteindre en fin de compte le besoin réel en matière de puissance. Les actionneurs servent de liaison entre la structure principale et la masse de TMD, mais à l’inverse d’autres systèmes de contrôle (voir fig. 1), ils ne sont pas utilisés pour contrôler directement la masse du TMD comme le ferait un actionneur de masse actif ou un système d’amortisseurs typiques.
Pour l’ADA à double usage intégré, une masse réactionnelle de 240 t a été choisie pour le fonctionnement passif. Pour le mode excitation, deux entraînements linéaires, un pour chacune des directions principales, sont fixés à la masse du TMD, avec des pivots placés à proximité du centre de gravité de la masse pour éviter les artefacts torsionnels. Chacun des entraînements linéaires peut fournir une force maximale de 40 kN dans une plage de +/- 600 mm maxi (voir détails sur la fig. 2). Les entraînements linéaires peuvent être détachés, de manière à ce que l’intégralité du mode passif ne soit pas influencée par les paliers des actionneurs pour le cas improbable où les paliers seraient défaillants.


Figure 10 – Types de systèmes de contrôle – TMD à double usage comparé à des systèmes passifs, semi-actifs, actifs et hybrides
Le système est équipé de quatre accéléromètres monoaxes (seismic K-Beam/MEMS ; un dans chaque direction) afin de déterminer les accélérations au niveau du sommet de la tour et de la masse du TMD. Les signaux d’accélération sont dotés de filtres passe-bande à l’intérieur de la plage des fréquences naturelles fondamentales de la tour (comprises entre 0,1 et 0,3 Hz) et intégrés pour obtenir la vitesse et le déplacement de la tour.
De plus, les valeurs de déplacement intégrées peuvent être comparées aux valeurs d’un système de mesure GPS complémentaire installé au sommet de la tour dans le but de comparer les dérives des signaux. Un test de corrélation initial a été réalisé en conséquence. Enfin, les déplacements de l’ADA sont surveillés à l’aide de transducteurs potentiométriques à fil et d’un système inductif de mesure de longueur intégré dans les moteurs linéaires.
7.0 Algorithme de contrôle
La boucle de contrôle générale de la tour est illustrée à la figure 5 : elle montre la séquence de contrôle de la boucle fermée. Un plan détaillé de l’algorithme de contrôle nécessiterait des modèles analytiques des actionneurs de la masse de l’ADA afin de déterminer la connexion entre l’entrée de l’actionneur et la force d’action appliquée. Un tel modèle devrait être associé au modèle analytique de la structure principale qui décrit le comportement dynamique global du bâtiment. De plus, en comparaison avec les algorithmes de contrôle standard ayant été appliqués à d’autres applications HMD comme dans [2],[3] ou examinés théoriquement comme dans [1] , l’algorithme de contrôle de cette application à cette tour a dû tenir compte de l’excitation contrôlée synchrone dans une direction principale et de la réduction des vibrations dans la direction perpendiculaire. La réponse dynamique étant majoritairement attendue dans les modes fondamentaux, une commande de rétroaction linéaire avec tous ses bénéfices devrait être appliquée pour ces deux tâches afin d’éviter toute instabilité. Pour la commande simple réalisée, la commande de rétroaction linéaire atténuant la réponse dynamique de la tour perpendiculaire à l’excitation règle l’actionneur adéquat à une somme linéaire pondérée spécifique calculée à partir de sept mesures dynamiques structurelles. Les mesures sont : Les accélérations de l’ADA et du sommet de la tour, les vitesses de l’ADA et du sommet de la tour, les déplacements absolues de l’ADA et du sommet de la tour et le déplacement relatif de l’ADA et du sommet de la tour.
Il est important de noter que les facteurs de pondération présélectionnés sont des valeurs scalaires simples, positives ou négatives. Le paramétrage des facteurs de pondération se base sur les tests dynamiques de la tour et n’emploient aucune modification dépendante de la fréquence. La rétroaction de l’actionneur actif est calculée instantanément (à 50 Hz) et il s’agit encore d’une combinaison linéaire des mesures dynamiques précédentes. Aucun manipulation non-linéaire n’est employée. La conception de la commande a également été intégrée dans la simulation numérique d’un domaine temporel (comprendre intégration directe), afin de démontrer la performance de la réduction des vibrations de la commande de l’actionneur. Pour le mode excitation, le même principe a été employé pour la commande, avec une compensation du déplacement qui représente l’excitation de la tour à la valeur de déplacement souhaitée. La compensation est une fonction sinusoïdale basée sur la fréquence fondamentale détectée de chaque direction. La sortie de la commande servant à contrebalancer la variation du déplacement du sommet de la tour provoqué par d’autres perturbations est modulée par la fonction de compensation sinusoïdale et la valeur de la commande est adaptée en conséquence.

La commande de rétroaction linéaire servant à réduire la réponse dynamique de la tour perpendiculaire à l’excitation permet à la commande de la force vers l’actionneur d’être une somme linéaire pondérée spécifique calculée à partir des sept mesures dynamiques du programme. Les sept mesures sont les suivantes : Les accélérations de l’ADA et du sommet de la tour, les vitesses de l’ADA et du sommet de la tour, les déplacements absolues de l’ADA et du sommet de la tour et le déplacement relatif de l’ADA et du sommet de la tour. Il est important de noter que les facteurs de pondération sont des valeurs scalaires simples, positives ou négatives. Le paramétrage du facteur de pondération se base sur les tests dynamiques expérimentaux de la tour. La rétroaction de l’actionneur est activée, calculée instantanément (50 Hz)
et les facteurs de pondération sont scalaires et n’emploient aucune forme de fonction de transfert liée à la fréquence. La rétroaction est également une combinaison linéaire de la propriété dynamique. Aucun manipulation ou logique non-linéaire n’est employée. La conception de la commande a été intégrée pour une simulation numérique dans le domaine temporel (intégration directe), de sorte que pour chaque stade temporel, l’entrée de force au niveau de la masse du TMD comme commande de l’actionneur peut être adaptée. La figure 12 montre les résultats de la simulation concernant la suppression des vibrations, les déplacements de la tour et la course de la masse du TMD correspondante.


Pour le mode excitation, le même principe a été employé pour la commande, avec une compensation qui représente l’excitation de la tour à la valeur de déplacement souhaitée. La compensation est une fonction sinusoïdale basée sur la fréquence fondamentale détectée de chaque direction. La sortie de la commande servant à contrebalancer la variation du déplacement du haut de la tour provoquée par d’autres perturbations est modulée par la fonction de compensation sinusoïdale
et la valeur de la commande est adaptée en conséquence. Pour cette compensation, un facteur de pondération a été déterminé de manière expérimentale. La figure 13 montre les résultats numériques avec une perturbation liée à une charge de rafale en mode excitation avec une excitation sinusoïdale simple et un algorithme de contrôle appliqué.


8.0 Concept de sécurité
En considérant la force de +/- 40 kN pouvant être fournie par les entraînements linéaires utilisés comme actionneurs, un concept de sécurité est indispensable, afin de s’assurer que les déplacements de la tour n’excèdent pas la résistance en fatigue. Cette condition s’applique, même si la force appliquée n’est pas suffisante pour provoquer des déflexions supérieures aux valeurs prédéfinies de +/- 200 mm au sommet de la tour. L’une des approches visant à améliorer la sécurité du système a consisté à augmenter la redondance des capteurs de surveillance qui enregistrent la déflexion au sommet de la tour. Afin de réaliser au mieux cette tâche, un système de surveillance indépendant additionnel, utilisant idéalement un principe de mesure différent de celui du logiciel de contrôle actuel, a été intégré. Pour le projet présenté ici, le logiciel de contrôle emploie, comme mentionné, des accéléromètres et un niveau d’accélération pour le filtre passe-bande défini à l’intérieur de la plage de fréquences naturelles pertinentes de la structure. Le système de surveillance principal est un système mondial de navigation par satellites (GNSS) d’une précision de +/- 10 mm. Le système GNSS requiert une station de base servant de référence qui traite les coordonnées des valeurs de la réponse du déplacement réel. En cas de déplacement du sommet de la tour supérieur à un seuil prédéterminé pendant le mode d’excitation artificiel (ce phénomène pouvant être imputé à une excitation additionnelle par le vent ou autre), un relais commute le signal d’assistance sur 0 V. Ceci entraîne alors l’interruption du mode d’excitation. De plus, les deux systèmes de surveillance contrôlent en continu les données acquises pour s’assurer de l’absence de signaux défectueux des capteurs qui pourraient également entraîner l’interruption du mode d’excitation actif. Les signaux défectueux d’accélération/des transducteurs potentiométriques sont détectés par un critère de sélection d’un pic spectral : on peut supposer que les capteurs fournissent des signaux légitimes uniquement si la sélection du pic dans une plage pertinente est possible. Pendant que le système GNSS analyse le changement de coordonnées, si les données échantillonnées ne changent pas en temps opportun, le système suppose automatiquement que le signal est défectueux.
9.0 Tests de vibrations
Des tests de vibrations initiaux de la tour ont été réalisés avant que la tour ne soit achevée ; à ce stade, les fréquences fondamentales de la tour étaient ainsi supérieures à la plage de réglages spécifiée pour le système TMD passif. Le TMD est ajusté à la fréquence de réglage la plus élevée possible. L’objectif de ces tests de vibrations était de déterminer les fréquences fondamentales de la tour avec un système TMD bloqué, ainsi que l’amortissement structurel inhérent. De plus, le comportement dynamique avec un système TMD passif engagé devrait être déterminé, ainsi que l’augmentation de l’amortissement structurel lié au système d’ADA. Afin d’identifier les fréquences naturelles fondamentales de la tour, il est possible d’employer la méthode de densité spectrale de puissance moyenne normalisée (DSPMN) [1] . Pour cela, les historiques temporels enregistrés doivent être divisés en segments. Ces segments doivent être transformés en domaines de fréquences. Le spectre qui en résulte doit alors être normalisé, la moyenne doit être calculée et le résultat doit être multiplié par le spectre conjugué complexe.
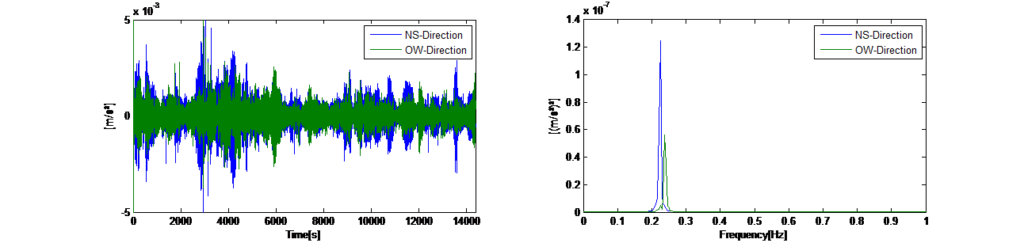
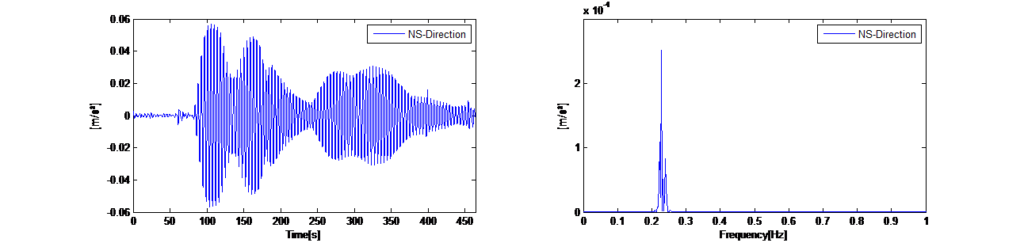
Cette méthode permet d’éliminer toutes les vibrations aléatoires et d’afficher uniquement les vibrations libres récurrentes de la structure dans le spectre moyen qui représente désormais les fréquences naturelles principales en excitation de la tour. La figure 14 de gauche indique les historiques temporels enregistrés des vibrations ambiantes horizontales dans les directions X et Y avec un TMD bloqué. La figure 14 de droite indique la moyenne du spectre d’auto-puissance correspondant pour une longueur de segment de 120 secondes. Le spectre montre que la tour présente une réponse dynamique à deux fréquences dominantes (0,225 Hz dans la direction X et 0,245 Hz dans la direction Y).
Outre la méthode de la moyenne du spectre de puissance décrite ci-dessus, qui suppose que l’excitation ambiante entraîne une réponse dynamique suffisante en modes de vibrations dans l’intérêt d’augmenter la sécurité stochastique, les fréquences naturelles ont été déterminées à l’aide du logiciel commercial de traitement des signaux ARTEMIS [1] qui comprend une méthode de décomposition améliorée du domaine de fréquence et une méthode d’identification du sous-espace stochastique.

La méthode de décomposition améliorée du domaine de fréquence et la méthode d’identification du sous-espace stochastique sont des techniques largement utilisées pour l’identification des paramètres modaux qui concernent uniquement la sortie.


La méthode de décomposition améliorée du domaine de fréquence repose sur le calcul du spectre de réponses. Des enregistrements longs sont ainsi nécessaires pour maintenir un faible taux d’erreurs concernant l’estimation du spectre et pour permettre une extraction fiable des paramètres modaux. L’algorithme d’identification du sous-espace stochastique a été appliqué afin d’identifier des passerelles à l’aide d’un modèle qui concerne uniquement la sortie. Les méthodes d’identification du sous-espace stochastique fonctionnent sous forme de domaines temporels et se basent sur une description de l’espace-état du problème dynamique. Les résultats de l’identification du système à différents ordres du modèle sont comparés afin de distinguer les modes structurels réels des modes simulés dans les diagrammes de stabilisation. Ces diagrammes sont une méthode appréciée de sélection du modèle de système, car les modes structurels réels tendent à rester stables pour les ordres de modèles successifs et remplissent certains critères de stabilisation évalués dans des procédures automatisées. La figure 15 montre une fiche de stabilité pour des données ambiantes enregistrées à partir desquelles les modes pertinents n’ont pas pu être déterminés. Les modes identifiés et les ratios d’amortissement déterminés pour chaque mode avec TMD bloqué (à gauche) et TMD activé (à droite) sont également illustrés sur la figure 14. Une augmentation de l’amortissement structurel peut être observée. L’amortissement structurel additionnel se trouve dans la plage de valeurs théoriques pouvant être déterminées à partir du modèle théorique pour lequel le réglage de TMD désaccordé a été envisagé.
Outre les tests de vibrations ambiantes avec le système de TMD passif, des tests préliminaires avec le mode d’excitation actif ont été réalisés, alors que le système TMD était désaccordé. La figure 12 de gauche illustre l’historique temporel des accélérations enregistrées au sommet de la tour. Après l’excitation sinusoïdale initiale, l’algorithme permettant d’atteindre un niveau d’accélération constant a été activé, afin de déterminer de manière expérimentale la corrélation entre la déflexion de la tour et le déplacement forcé de la masse du TMD. L’historique temporel illustré à la figure 12 montre les deux scénarios d’essai en mode d’excitation et le spectre TFD correspondant montre la réponse claire de la tour dans ses deux fréquences fondamentales (directions X et Y). La section temporelle marquée en vert correspond à une excitation sinusoïdale de la masse avec commande active désactivée ayant entraîné une réponse dynamique dans les deux directions principales. Le spectre TFD qui en résulte montre les deux pics permettant d’identifier les fréquences fondamentales dans ces deux directions. Le segment temporel marqué en bleu correspond à une excitation avec commande active activée ayant entraîné un déplacement plus constant de la tour, principalement dans une direction. La réduction des vibrations inhérentes une fois le mode d’excitation désactivé a également été utilisée pour déterminer l’amortissement structurel défini à D = 2,4 %. Ce résultat corrèle le ratio d’amortissement déterminé avec les algorithmes d’identification des sous-espaces stochastiques.

10.0 Conclusion et perspectives
Un ADA à double usage a été installé sur la tour de test Thyssen Krupp d’une hauteur de 246 m, avec pour objectif de pouvoir exciter artificiellement la tour et ainsi d’obtenir une réponse dynamique contrôlée dans ses fréquences fondamentales. L’objectif de cette excitation est d’obtenir une oscillation définie du bâtiment dans les deux directions principales de la tour. Sur la base de calculs numériques, il a été déterminé qu’une masse de TMD de 240 t était nécessaire pour atteindre l’amortissement supplémentaire requis pour le mode passif et générer la force de contrôle requise permettant d’obtenir un déplacement du haut de la tour de +/- 200 mm. Afin de créer un niveau de déplacement constant en mode d’excitation et d’éliminer les déplacements provoqués par les vents et les composants à l’origine des vibrations forcées dans la direction perpendiculaire, un algorithme de contrôle a été développé et testé à l’aide de simulations numériques. Après l’installation du système d’ADA passif de type pendulaire pour lequel des dalles de béton préfabriquées ont été utilisées afin de servir de masse réactionnelle, les actionneurs ont été commandés et des tests initiaux ont été réalisés. Les tests ont révélé que l’amortissement inhérent de la tour était plus élevé que ce qui avait été anticipé, mais que tous les modes pertinents pouvaient être clairement déterminés. Le système d’excitation actif du bâtiment a pu être testé et il fonctionne convenablement. Le bâtiment n’étant pas encore entièrement achevé à ce moment, il n’a cependant pas été testé dans toute son ampleur pour permettre d’obtenir l’ensemble des paramètres de fonctionnement. En raison de l’état inachevé du bâtiment, le TMD passif n’a pas pu être adapté aux fréquences fondamentales déterminées.
Une fois que le système d’amortissement sera ajusté, des tests supplémentaires du bâtiment seront réalisés. Ils incluront également des tests concernant l’amortissement en fonction de l’amplitude et l’intégration des systèmes de sécurité.
RÉFÉRENCES
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
1.0 Introduction/ historique
Une tour de 246 m a été érigée au sud-ouest de l’Allemagne avec pour objectif d’accueillir un centre de test et d’innovations dans le domaine des ascenseurs. La tour, qui a une géométrie circulaire avec un diamètre de 20 m, offre suffisamment d’espace pour 9 gaines d’essai, un ascenseur de secour en cas d’incendie et un ascenseur panoramique. En complément, une gaine de 220 m est destiné à être utilisé comme monte charge pour les programmes d’essai.
La base de la tour, de 40 m de diamètre, offre un espace supplémentaire pour des établissements de services, un hall d’entrée et un centre éducatif. A une hauteur de 232 m, une plateforme d’observation (la plus haute d’Allemagne) offre une vue spectaculaire sur la Forêt-Noire et sur les Alpes par temps dégagé.

2.0 Système structurel
Pour l’essentiel, la structure de la tour est constitué d’un tube en béton armé, d’un diamètre de 20,8 m, ancré à une profondeur de 30 m dans le sol environnant (voir figure 2). Jusqu’à une hauteur de 110 m, l’épaisseur du tube est de 40 cm. Au-delà, elle est de 25 cm. Le sol, composé d’une couche de Keuper et de calcaire coquillier, présente une portance élevée, permettant une fondation sur radier. Outre l’ancrage dans le sol environnant, la base plus élargie de la tour offre une rigidité latérale supplémentaire.
La rigidité du tube en béton est principalement apportée par les parois des gaines d’ascenseurs. Des dalles de plancher préfabriquées ont été installées seulement à certains niveaux, afin d’offrir un accès aux gaines d’ascenseurs. Certaines des gaines d’ascenseurs se terminent à un niveau de 115 m et sont recouvertes par une dalle de grande portée coulée en place, d’une épaisseur de 40 cm. Ces étages sont utilisés pour les espaces de bureaux. Au-dessus, un espace vide allant jusqu’à un niveau de 197 m est utilisé comme réservoir de chaleur et pour le système d’ADA. Le haut de la tour est utilisé comme espace de bureau et pour les gaines d’ascenseurs restantes.

L’une des caractéristiques distinctives de la tour de test est sa façade textile, consistant en une maille de fibre de verre recouverte de PTFE. À mesure que l’on monte dans le bâtiment, la largeur d’ouverture de la maille augmente, et avec elle également la transparence de la façade, tandis que la densité et donc le poids du matériau diminuent, améliorant aussi ses propriétés aérodynamiques.
La façade spiralée forme une hélice de Scruton et la toile la composant aide à protéger la structure en béton du soleil, afin de réduire le stress thermique provoqué par les radiations. Pour la conception de la façade et le choix du matériau, les paramètres pris en compte sont l’entretien, la durabilité et la charge de vent.
3.0 Méthode de construction

La tour de test a été érigée selon les étapes suivantes :
- Excavation d’une fosse circulaire de 30 m pour la base de la tour. L’excavation et la forme ont été obtenues grâce à une explosion initiale. Après les travaux d’excavation, la fosse a été sécurisée à l’aide de tirants d’ancrage et d’une paroi en béton projeté.
- Coulage du radier
- Construction du noyau béton verticale à l’aide d’un coffrage coulissant. Les parois ont toutes été construites dans le cadre d’un processus continu sur une période de 4 mois.
- Construction des dalles de plancher.
- Construction de la zone du hall d’entrée.
4.0 Réponse dynamique sous charge de vent
Les fréquences fondamentales de la tour de test prévues étaient de l’ordre de 0,17 Hz à 0,20 Hz par seconde, en fonction de la phase de la construction et de l’état du béton (fissuré/non fissuré), voir figure 4.

L’étude sous vents a révélée que des vents atteignant une vitesse au sol (à une hauteur de 10 m) de l’ordre de 55 à 60 km/h pouvaient entraîner la mise en résonance de la structure. Il était attendu que, sans amortissement supplémentaire, cette mise en résonnance provoquerait des déflexions d’environ +/- 750 mm au sommet de la structure, entraînant d’une part une gêne pour les occupants, et d’autre part une sollicitation significative en fatigue de la structure en béton de la tour (voir figure 5). Afin de réduire la réponse dynamique à l’excitation provoquée par les vents latéraux, un système d’amortisseur dynamique accordé passif a été mis en place. La tour devant servir de tour d’essai pour des ascenseurs destinés à des bâtiments sensibles aux oscillations, le propriétaire cherchait la possibilité d’exciter artificiellement la tour par temps calme, sans que ces mouvements ne provoquent de problèmes liés à la fatigue. Le niveau requis pour les mouvements d’oscillation artificiels était d’approximativement +/- 200 mm, cette plage étant considérée comme sécuritaire. Cette demande nous a offert l’opportunité rare de mettre en place un système d’amortisseur à masse hybride (Hybrid Mass Damper, HMD) ou, le concept étant dévié d’autres systèmes HMD introduits par le passé, un ADA (Tuned Mass Damper, TMD) à double usage. Le système sera présenté dans les chapitres suivants, ainsi que l’optimisation du système passif, la conception du mécanisme de l’actionneur, les algorithmes de contrôle et le concept de sécurité.

5.0 Optimisation du système d'amortisseur dynamique accordé passif
Les paramètres du système TMD passif doivent être déterminés en fonction de trois aspects distincts : a) ils doivent fournir un amortissement structurel supplémentaire suffisant visant à réduire la réponse dynamique liée à l’excitation provoquée par les tourbillons ; b) ils doivent limiter le déplacement de la masse principale du TMD en mode passif à une valeur atteignable/pratique lorsqu’elle est soumise à une excitation provoquée par des rafales de vents latéraux ; c) ils doivent permettre de choisir la masse du TMD en fonction de l’apport énergétique nécessaire à la déflexion maximale souhaitée de la tour en mode d’excitation, en tenant compte de l’enveloppe de performances permise par les actionneurs fournis (p. ex. force générée maximale et course maximale pendant le fonctionnement). Afin d’optimiser l’ADA, un modèle numérique a été utilisé : il représente la distribution de la masse de la tour et les couples d’inertie tels qu’ils sont reportés dans les propriétés structurelles identifiées. Les éléments rigides entre étages ont également été ajustés afin de correspondre aux formes et aux fréquences naturelles relevées à partir d’observations complèmentaires. La fig. 6 de gauche montre les formes et fréquences naturelles de ce modèle analogue employé. La figure 6 de gauche compare également les formes du modèle analogue à celles du modèle détaillé préparé par le consultant en structures.


A noter que le TMD a été modelé de façon discrète en tant que système de type pendulaire occupant une place excentrique sur la tour. Les caractéristiques des charges entrantes applicables, c’est à dire l’excitation en résonance provoquée par les tourbillons, sont très similaires à celles d’une excitation harmonique unique. Or, la charge de rafale coexistante est inhérente à sa nature stochastique. C’est pourquoi des critères d’optimisation autres que le très célèbre critère de Den Hartog s’appliquent. De plus, les déplacements relatifs du TMD sont plus importants pour une charge de nature stochastique que pour une charge de type harmonique. Une charge proche de la réalité doit être considérée pour la détermination numérique des paramètres optimaux du TMD. C’est pourquoi un historique temporel a été généré, incluant à la fois les charges de rafales stochastiques (basées sur le spectre de Davenport) et un composant résonnant superposé semblable à un tourbillon, afin de représenter l’excitation globale provoquée par les vents latéraux (voir fig. 3, à droite). La réduction des déplacements de la tour pouvant être obtenue grâce au système TMD passif optimisé, ainsi que les déplacements du TMD correspondants, sont illustrés dans la figure 3, à droite. En se basant sur ces résultats, pour un amortissement structurel inhérent estimé à ξ = 0,8 %, il a été déterminé qu’un TMD d’une masse de 240 t était nécessaire pour maintenir les déplacements dans une plage de +/- 650 mm tout en conservant un ratio d’amortissement du TMD optimal offrant les meilleures performances de ce dernier. Un amortissement plus élevé aurait pu permettre de réduire la course tout en gardant une efficacité suffisante, mais cela aurait impacté négativement les exigences en matière de force de l’actionneur. Afin de déterminer les forces nécessaires pour un réglage optimal de l’ADA de 240 t, l’utilisation du modèle analogue a également permis de s’assurer qu’une force maximale de 40 kN des actionneurs permettait d’atteindre une plage de déflexions de la tour de +/- 200 mm. La figure 4 montre les résultats de la simulation numérique dans le domaine temporel sur le modèle numérique analogue ; y sont représentées : les déflexions au niveau du sommet de la tour, les déplacements de la masse de l’ADA et les forces entrantes actives à l’origine de ces déplacements.


6.0 Description du système de contrôle
Le double usage du système de contrôle sert : a) à réduire la consommation d’énergie tout en réduisant les vibrations en fonctionnement passif normal et b) à réduire la puissance d’actionneur nécessaire grâce à l’utilisation des effets de résonnance, afin d’exciter la masse de l’ADA et atteindre en fin de compte le besoin réel en matière de puissance. Les actionneurs servent de liaison entre la structure principale et la masse de TMD, mais à l’inverse d’autres systèmes de contrôle (voir fig. 1), ils ne sont pas utilisés pour contrôler directement la masse du TMD comme le ferait un actionneur de masse actif ou un système d’amortisseur typiques. Pour le TMD à double usage intégré, une masse réactionnelle de 240 t a été choisie pour le fonctionnement passif. Pour le mode excitation, deux entraînements linéaires, un pour chacune des directions principales, sont fixés à la masse du TMD, avec des pivots placés à proximité du centre de gravité de la masse pour éviter les artefacts torsionnels. Chacun des entraînements linéaires peut fournir une force maximale de 40 kN dans une plage de +/- 600 mm maxi (voir détails sur la fig. 2). Les entraînements linéaires peuvent être détachés, de manière à ce que l’intégralité du mode passif ne soit pas influencée par les paliers des actionneurs pour le cas improbable où les paliers seraient défaillants.


Le système est équipé de quatre accéléromètres monoaxes (seismic K-Beam/MEMS ; un dans chaque direction) afin de déterminer les accélérations au niveau du sommet de la tour et de la masse du TMD. Les signaux d’accélération sont dotés de filtres passe-bande à l’intérieur de la plage des fréquences naturelles fondamentales de la tour (comprises entre 0,1 et 0,3 Hz) et intégrés pour garantir la vélocité et la déflexion de la tour. De plus, les valeurs de déplacement intégrées peuvent être comparées aux valeurs d’un système mondial de navigation par satellites complémentaire également installé au sommet de la tour dans le but de comparer les dérives des signaux. Un test de corrélation initial a été réalisé en conséquence. Enfin, les déplacements de l’ADA sont surveillés à l’aide de transducteurs potentiométriques à fil et d’un système inductif de mesure de longueur intégré dans les moteurs linéaires.
7.0 Algorithme de contrôle
La boucle de contrôle générale de la tour est illustrée à la figure 5 : elle montre la séquence de contrôle de la boucle fermée. Un plan détaillé de l’algorithme de contrôle nécessiterait des modèles analytiques des actionneurs de la masse de l’ADA afin de déterminer la connexion entre l’entrée de l’actionneur et la force d’action appliquée. Un tel modèle devrait être associé au modèle analytique de la structure principale qui décrit le comportement dynamique global du bâtiment. De plus, en comparaison avec les algorithmes de contrôle standard ayant été appliqués à d’autres applications HMD comme dans [2],[3] ou examinés théoriquement comme dans [1] , l’algorithme de contrôle de cette application à cette tour a dû tenir compte de l’excitation contrôlée synchrone dans une direction principale et de la réduction des vibrations dans la direction perpendiculaire. La réponse dynamique étant majoritairement attendue dans les modes fondamentaux, une commande de rétroaction linéaire avec tous ses bénéfices devrait être appliquée pour ces deux tâches afin d’éviter toute instabilité. Pour la commande simple réalisée, la commande de rétroaction linéaire atténuant la réponse dynamique de la tour perpendiculaire à l’excitation règle l’actionneur adéquat à une somme linéaire pondérée spécifique calculée à partir de sept mesures dynamiques structurelles. Les mesures sont : Les accélérations du TMD et du sommet de la tour, les vélocités du TMD et du sommet de la tour, les déplacements du TMD et du sommet de la tour et le déplacement relatif du TMD du sommet de la tour. Il est important de noter que les facteurs de pondération présélectionnés sont des valeurs scalaires simples, positives ou négatives. Le paramétrage des facteurs de pondération se base sur les tests dynamiques de la tour et n’emploient aucune modification dépendante de la fréquence. La rétroaction de l’actionneur actif est calculée instantanément (à 50 Hz) et il s’agit encore d’une combinaison linéaire des mesures dynamiques précédentes. Aucun manipulation non-linéaire n’est employée. La conception de la commande a également été intégrée dans la simulation numérique d’un domaine temporel (comprendre intégration directe), afin de démontrer la performance de la réduction des vibrations de la commande de l’actionneur. Pour le mode excitation, le même principe a été employé pour la commande, avec une compensation du déplacement qui représente l’excitation de la tour à la valeur de déplacement souhaitée. La compensation est une fonction sinusoïdale basée sur la fréquence fondamentale détectée de chaque direction. La sortie de la commande servant à contrebalancer la variation du déplacement du sommet de la tour provoqué par d’autres perturbations est modulée par la fonction de compensation sinusoïdale et la valeur de la commande est adaptée en conséquence.

La commande de rétroaction linéaire servant à réduire la réponse dynamique de la tour perpendiculaire à l’excitation permet à la commande de la force vers l’actionneur d’être une somme linéaire pondérée spécifique calculée à partir des sept mesures dynamiques du programme. Les sept mesures sont les suivantes : Les accélérations de l’ADA et du sommet de la tour, les vitesses de l’ADA et du sommet de la tour, les déplacements absolues de l’ADA et du sommet de la tour et le déplacement relatif de l’ADA et du sommet de la tour. Il est important de noter que les facteurs de pondération sont des valeurs scalaires simples, positives ou négatives. Le paramétrage du facteur de pondération se base sur les tests dynamiques expérimentaux de la tour. La rétroaction de l’actionneur est activée, calculée instantanément (50 Hz) et les facteurs de pondération sont scalaires et n’emploient aucune forme de fonction de transfert liée à la fréquence. La rétroaction est également une combinaison linéaire de la propriété dynamique. Aucun manipulation ou logique non-linéaire n’est employée. La conception de la commande a été intégrée pour une simulation numérique dans le domaine temporel (intégration directe), de sorte que pour chaque stade temporel, l’entrée de force au niveau de la masse du TMD comme commande de l’actionneur peut être adaptée. La figure 12 montre les résultats de la simulation concernant la suppression des vibrations, les déplacements de la tour et la course de la masse du TMD correspondante.


Pour le mode excitation, le même principe a été employé pour la commande, avec une compensation qui représente l’excitation de la tour à la valeur de déplacement souhaitée. La compensation est une fonction sinusoïdale basée sur la fréquence fondamentale détectée de chaque direction. La sortie de la commande servant à contrebalancer la variation du déplacement du sommet de la tour provoquée par des perturbations est modulée par la fonction de compensation sinusoïdale et la valeur de la commande doit être adaptée en conséquence. Pour cette compensation, un facteur de pondération a été déterminé de manière expérimentale. La figure 13 montre les résultats numériques avec une perturbation liée à une charge de rafale en mode excitation avec une excitation sinusoïdale simple et un algorithme de contrôle appliqué.


8.0 Concept de sécurité
En considérant la force de +/- 40 kN pouvant être fournie par les entraînements linéaires utilisés comme actionneurs, un concept de sécurité est indispensable, afin de s’assurer que les déplacements de la tour n’excèdent pas la résistance en fatigue. Cette condition s’applique, même si la force appliquée n’est pas suffisante pour provoquer des déflexions supérieures aux valeurs prédéfinies de +/- 200 mm au sommet de la tour. L’une des approches visant à améliorer la sécurité du système a consisté à augmenter la redondance des capteurs de surveillance qui enregistrent la déflexion au sommet de la tour. Afin de réaliser au mieux cette tâche, un système de surveillance indépendant additionnel, utilisant idéalement un principe de mesure différent de celui du logiciel de contrôle actuel, a été intégré. Pour le projet présenté ici, le logiciel de contrôle emploie, comme mentionné, des accéléromètres et un niveau d’accélération pour le filtre passe-bande défini à l’intérieur de la plage de fréquences naturelles pertinentes de la structure. Le système de surveillance principal est un système mondial de navigation par satellites (GNSS) d’une précision de +/- 10 mm. Le système GNSS requiert une station de base servant de référence qui traite les coordonnées des valeurs de la réponse du déplacement réel. En cas de déplacement du sommet de la tour supérieur à un seuil prédéterminé pendant le mode d’excitation artificiel (ce phénomène pouvant être imputé à une excitation additionnelle par le vent ou autre), un relais commute le signal d’assistance sur 0 V. Ceci entraîne alors l’interruption du mode d’excitation. De plus, les deux systèmes de surveillance contrôlent en continu les données acquises pour s’assurer de l’absence de signaux défectueux des capteurs qui pourraient également entraîner l’interruption du mode d’excitation actif. Les signaux défectueux d’accélération/des transducteurs potentiométriques sont détectés par un critère de sélection d’un pic spectral : on peut supposer que les capteurs fournissent des signaux légitimes uniquement si la sélection du pic dans une plage pertinente est possible. Pendant que le système GNSS analyse le changement de coordonnées, si les données échantillonnées ne changent pas en temps opportun, le système suppose automatiquement que le signal est défectueux.
9.0 Tests de vibrations
Des tests de vibrations initiaux de la tour ont été réalisés avant que la tour ne soit achevée ; à ce stade, les fréquences fondamentales de la tour étaient ainsi supérieures à la plage de réglages spécifiée pour le système TMD passif. Le TMD est ajusté à la fréquence de réglage la plus élevée possible. L’objectif de ces tests de vibrations était de déterminer les fréquences fondamentales de la tour avec un système TMD bloqué, ainsi que l’amortissement structurel inhérent. De plus, le comportement dynamique avec un système TMD passif engagé devrait être déterminé, ainsi que l’augmentation de l’amortissement structurel lié au système d’ADA. Afin d’identifier les fréquences naturelles fondamentales de la tour, il est possible d’employer la méthode de densité spectrale de puissance moyenne normalisée (DSPMN) [1] . Pour cela, les historiques temporels enregistrés doivent être divisés en segments. Ces segments doivent être transformés en domaines de fréquences. Le spectre qui en résulte doit alors être normalisé, la moyenne doit être calculée et le résultat doit être multiplié par le spectre conjugué complexe.
Cette méthode permet d’éliminer toutes les vibrations aléatoires et d’afficher uniquement les vibrations libres récurrentes de la structure dans le spectre moyen qui représente désormais les fréquences naturelles principales en excitation de la tour. La figure 14 de gauche indique les historiques temporels enregistrés des vibrations ambiantes horizontales dans les directions X et Y avec un TMD bloqué. La figure 14 de droite indique la moyenne du spectre d’auto-puissance correspondant pour une longueur de segment de 120 secondes. Le spectre montre que la tour présente une réponse dynamique à deux fréquences dominantes (0,225 Hz dans la direction X et 0,245 Hz dans la direction Y).
Outre la méthode de la moyenne du spectre de puissance décrite ci-dessus, qui suppose que l’excitation ambiante entraîne une réponse dynamique suffisante en modes de vibrations dans l’intérêt d’augmenter la sécurité stochastique, les fréquences naturelles ont été déterminées à l’aide du logiciel commercial de traitement des signaux ARTEMIS [1] qui comprend une méthode de décomposition améliorée du domaine de fréquence et une méthode d’identification du sous-espace stochastique.

La méthode de décomposition améliorée du domaine de fréquence et la méthode d’identification du sous-espace stochastique sont des techniques largement utilisées pour l’identification des paramètres modaux qui concernent uniquement la sortie.


La méthode de décomposition améliorée du domaine de fréquence repose sur le calcul du spectre de réponses. Des enregistrements longs sont ainsi nécessaires pour maintenir un faible taux d’erreurs concernant l’estimation du spectre et pour permettre une extraction fiable des paramètres modaux. L’algorithme d’identification du sous-espace stochastique a été appliqué afin d’identifier des passerelles à l’aide d’un modèle qui concerne uniquement la sortie. Les méthodes d’identification du sous-espace stochastique fonctionnent sous forme de domaines temporels et se basent sur une description de l’espace-état du problème dynamique. Les résultats de l’identification du système à différents ordres du modèle sont comparés afin de distinguer les modes structurels réels des modes simulés dans les diagrammes de stabilisation. Ces diagrammes sont une méthode appréciée de sélection du modèle de système, car les modes structurels réels tendent à rester stables pour les ordres de modèles successifs et remplissent certains critères de stabilisation évalués dans des procédures automatisées. La figure 15 montre une fiche de stabilité pour des données ambiantes enregistrées à partir desquelles les modes pertinents n’ont pas pu être déterminés. Les modes identifiés et les ratios d’amortissement déterminés pour chaque mode avec TMD bloqué (à gauche) et TMD activé (à droite) sont également illustrés sur la figure 14. Une augmentation de l’amortissement structurel peut être observée. L’amortissement structurel additionnel se trouve dans la plage de valeurs théoriques pouvant être déterminées à partir du modèle théorique pour lequel le réglage de l’ADA désaccordé a été envisagé. Outre les tests de vibrations ambiantes avec le système d’ADA passif, des tests préliminaires avec le mode d’excitation actif ont été réalisés, alors que le système était désaccordé. La figure 12 de gauche illustre l’historique temporel des accélérations enregistrées au sommet de la tour. Après l’excitation sinusoïdale initiale, l’algorithme permettant d’atteindre un niveau d’accélération constant a été activé, afin de déterminer de manière expérimentale la corrélation entre la déflexion de la tour et le déplacement forcé de la masse du TMD. L’historique temporel illustré à la figure 12 montre les deux scénarios d’essai en mode d’excitation et le spectre TFD correspondant montre la réponse claire de la tour dans ses deux fréquences fondamentales (directions X et Y). La section temporelle marquée en vert correspond à une excitation sinusoïdale de la masse avec commande active désactivée ayant entraîné une réponse dynamique dans les deux directions principales. Le spectre TFD qui en résulte montre les deux pics permettant d’identifier les fréquences fondamentales dans ces deux directions. Le segment temporel marqué en bleu correspond à une excitation avec commande active activée ayant entraîné un déplacement plus constant de la tour, principalement dans une direction. La réduction des vibrations inhérentes une fois le mode d’excitation désactivé a également été utilisée pour déterminer l’amortissement structurel défini à D = 2,4 %. Ce résultat corrèle le ratio d’amortissement déterminé avec les algorithmes d’identification des sous-espaces stochastiques.

10.0 Conclusion et perspectives
Un ADA à double usage a été installé sur la tour de test Thyssen Krupp d’une hauteur de 246 m, avec pour objectif de pouvoir exciter artificiellement la tour et ainsi d’obtenir une réponse dynamique contrôlée dans ses fréquences fondamentales. L’objectif de cette excitation est d’obtenir une oscillation définie du bâtiment dans les deux directions principales de la tour. Sur la base de calculs numériques, il a été déterminé qu’une masse de TMD de 240 t était nécessaire pour atteindre l’amortissement supplémentaire requis pour le mode passif et générer la force de contrôle requise permettant d’obtenir un déplacement du haut de la tour de +/- 200 mm. Afin de créer un niveau de déplacement constant en mode d’excitation et d’éliminer les déplacements provoqués par les vents et les composants à l’origine des vibrations forcées dans la direction perpendiculaire, un algorithme de contrôle a été développé et testé à l’aide de simulations numériques. Après l’installation du système d’ADA passif de type pendulaire pour lequel des dalles de béton préfabriquées ont été utilisées afin de servir de masse réactionnelle, les actionneurs ont été commandés et des tests initiaux ont été réalisés. Les tests ont révélé que l’amortissement inhérent de la tour était plus élevé que ce qui avait été anticipé, mais que tous les modes pertinents pouvaient être clairement déterminés. Le système d’excitation actif du bâtiment a pu être testé et il fonctionne convenablement. Le bâtiment n’étant pas encore entièrement achevé à ce moment, il n’a cependant pas été testé dans toute son ampleur pour permettre d’obtenir l’ensemble des paramètres de fonctionnement. En raison de l’état inachevé du bâtiment, le TMD passif n’a pas pu être adapté aux fréquences fondamentales déterminées.
Une fois que le système d’amortissement sera ajusté, des tests supplémentaires du bâtiment seront réalisés. Ils incluront également des tests concernant l’amortissement en fonction de l’amplitude et l’intégration des systèmes de sécurité.
RÉFÉRENCES
[1] Wenzel, H., Pichler, D., Schedler, R. (1991). „Ambiente Schwingungsmessungen zur System und Schadenserkennung an Tragwerken“, Bauingenieur 74
[2] Döhler, M., Andersen, P.: Mevel, L. (2012). “Operational Modal Analysis using a Fast Stochastic Subspace Identification Method”, Conference Proceedings of the Society for Experimental Mechanics Series
[3] Soong, T.T., Spencer, J.R. (2000). “Active, Semi-Active and hybrid control of structures” In 12th World Conference for Earthquake Engineering
[4] Ricciardelli, F.; Pizzimenti, A.D.; Mattei, M. (2003). Passive and active mass damper control of the response of tall buildings to wind gustiness. Eng. Struct., 25, 1199–1209
[5] Yang, N.Y.; Agrawal, A.K.; Samali, B.; Wu, J.C. Benchmark Problem for Response Control of Wind-Excited Tall Buildings. J. Eng. Mech. 2004, 130, 437–446.
[6] Watakabe, M.; Tohdp, M.; Chiba, O.; Izumi, N.; Ebisawa, H.; Fujita, T. Response control performance of a hybrid mass damper applied to a tall building. Earthq. Eng. Struct. Dyn. 2001, 30, 1655–1676.
[7] Tan, P.; Liu, Y.; Zhou, F.; Teng, J. Hybrid Mass Dampers for Canton Tower. CTBUH J. 2012, 24–29.
[8] Soong, T.T. “Active Structural Control: Theory and Practice”; John Wiley & Sons, Inc.: New York, NY, USA, 1990
[9] Preumont, A., Kazuto, S. (2008).”Active Control of Structures”, Wiley, Padstow
Partager cet article
Ressources supplémentaires
Vous souhaitez de plus amples informations à ce sujet ?
N'hésitez pas à nous contacter et à nous poser vos questions.
L'un de nos ingénieurs projet vous répondra dans les plus brefs délais.
Ressources supplémentaires
Vous souhaitez de plus amples informations à ce sujet ?
N'hésitez pas à nous contacter et à nous poser vos questions.
L'un de nos ingénieurs projet vous répondra dans les plus brefs délais.